Probabilità 4 - Option Club

Vi sono molte situazioni aleatorie che non possono essere interpretate, sensatamente, alla stregua di eventi elementari logicamente equivalenti. Una definizione di probabilità, empirica ma che ben si accorda col nostro intuito, per alcuni tipi di eventi ripetibili, è la seguente:

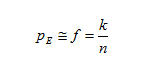
ove:

pE ..è la probabilità dell'evento E
f ...è la frequenza relativa
k...è il umero di prove che hanno avuto quell'esito (frequenza assoluta)
n...è il numero totale di prove

in cui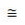significa « è approssimativamente uguale a », e l' approssimazione diventa sempre più piccola via via che cresce il numero delle prove.

La probabilità è il valore costante intorno al quale tende a stabilizzarsi la frequenza relativa di un evento al crescere del numero delle prove di un dato esperimento.

A questa "legge", la cui validità è rilevabile sperimentalmente, si è attribuito il nome di "legge empirica del caso". Essa stabilisce una stretta connessione tra probabilità calcolata a priori e probabilità stimata a posteriori.

Quando per esempio si lancia più volte una moneta, anche se all’inizio potrà prevalere il risultato “testa” piuttosto che “croce”, all’aumentare dei lanci la frequenza relativa delle uscite “testa” tenderà a eguagliare sempre più le uscite “croce”; finché, dopo migliaia di lanci, la frequenza relativa delle “teste” e delle “croci” andrà a stabilizzarsi attorno al valore 0,50 per entrambe.

Scaricate il programma sotto riportato e fate delle prove.

A proposito della legge empirica del caso

La legge empirica del caso, alle volte detta anche legge dei grandi numeri, viene applicata spesso in alcuni giochi in modo scorretto.

Un tipico esempio è quello del giocatore del Lotto che spera di fare strepitose vincite puntando sui numeri ritardatari, convinzione alimentata anche in maniera impropria da chi gestisce il gioco del Lotto in Italia.

Il ragionamento - naturalmente sbagliato - che fa il giocatore è il seguente. Poiché ogni numero del Lotto deve uscire in media ogni 18 estrazioni, e poiché per la legge empirica del caso, per n che tende all’infinito, la sua frequenza relativa deve essere uguale ad 1/18, allora, visto che non esce da varie estrazioni, prima o poi deve uscire, quindi lo gioco.

La conclusione: “ e quindi lo gioco”, equivale a dire: “ quindi la probabilità che esca alla prossima estrazione è maggiore di 1/18”.

Tali giocatori dovrebbero ricordare più spesso che «il caso non ha memoria». Se in 10 lanci di una moneta, tutti avvenuti nelle medesime condizioni, si è sempre verificato l’evento faccia "testa" nell’undicesimo lancio la faccia "testa" ha sempre probabilità 50% di verificarsi perché il caso - non avendo memoria - non ricorda ciò che è avvenuto nei dieci lanci precedenti.  

Resta comunque difficile - per esperienza personale -  convincere le persone che praticano questo gioco che non è affatto vero che i numeri con maggiore ritardo abbiano più probabilità di uscire rispetto agli altri.

Indietro