Option Club
Calcolo Combinatorio
TEORIA
Calcolo Combinatorio
Permutazioni, disposizioni e combinazioni semplici
Le difficoltà che sorgono più frequentemente nel calcolo delle probabilità, in presenza di un numero finito di eventi elementari, consistono nel contare con precisione i casi possibili e favorevoli e nell’applicare correttamente le regole. Per superare queste difficoltà, occorre premettere qualche semplice ragionamento di calcolo combinatorio.

Permutazioni
Le permutazioni di n elementi sono i possibili raggruppamenti che si possono formare con gli n elementi considerati prendendoli ogni volta tutti insieme in maniera tale che ogni gruppo differisca dall’altro per l’ordine di successione degli elementi stessi.
Non vi lasciate impressionare da questa definizione.


Così, se vi sono 4 persone in attesa di occupare i loro posti a sedere intorno ad un tavolo, ciascuna distribuzione delle 4 persone costituisce una permutazione.
In questo specifico caso il numero delle permutazioni è pari a 24.
Tale numero può essere facilmente calcolato facendo un semplice ragionamento.
Inizialmente vi sono 4 posti liberi e 4 persone in piedi. Vi sono dunque 4 differenti modi di occupare il solo primo posto. Quando il primo posto è stato occupato, ne rimangono 3 da occupare (n - 1). Così come vi erano 4 differenti modi di occupare il primo posto, vi sono ora 3 differenti modi di occupare il secondo posto. Pertanto i modi possibili di occupare i primi due posti sono 4 x 3 = 12. Rimangono ancora 2 persone per occupare gli altri 2 posti. Il terzo posto può essere occupato da una di queste, il che significa che vi sono 2 diverse possibilità di occuparlo (n - 2). Infime, il quarto e ultimo posto può essere occupato in un solo modo.
Pertanto il numero totale di modi diversi di occupare i 4 posti a disposizione è uguale alla seguente serie di prodotti 4 x 3 x 2 x 1 che fa esattamente 24.
In generale diremo che il numero di permutazioni semplici di un gruppo di n elementi è dato dal prodotto che si ottiene moltiplicando n per tutti i numeri consecutivi decrescenti a partire da n, cioè:
![]()
Questo prodotto prende il nome di enne fattoriale e si indica con n seguito da un punto esclamativo: n! Possiamo dunque esprimere le permutazioni semplici con la seguente formula generale:
![]()
la quale ci dice che le permutazioni di n elementi sono uguali al fattoriale di n.
Immaginando che le 4 persone siano contrassegnate dalle lettere A, B, C e D le 24 permutazioni sono:
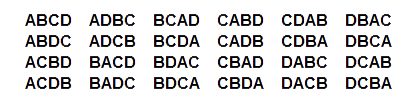
Naturalmente a noi interessa contare solo il numero dei diversi modi e non elencarli esplicitamente l'uno dopo l'altro come abbiamo fatto in questo caso.
Scopo del Calcolo combinatorio è evitare - appunto - elenchi inutili e noiosi ed arrivare al risultato richiesto con l'ausilio di calcoli molto semplici (le classiche 4 operazioni!). In questo senso il Calcolo combinatorio costituisce uno strumento aritmetico di supporto e in certi casi indispensabile nel Calcolo delle Probabilità poiché consente di determinare il numero di casi possibili (ma anche quelli favorevoli e contrari) che si possono verificare in una determinata prova.
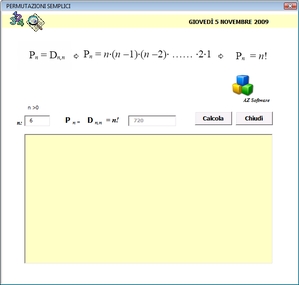
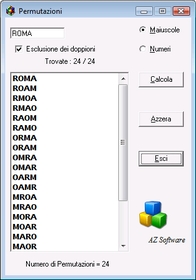
Esempio
Determinare tutti gli anagrammi della parola ROMA.
Gli anagrammi non sono altro che le permutazioni ottenute da una parola variando solo il posto delle lettere.
Il numero degli anagrammi richiesti della parola ROMA (composta da 4 lettere) sono pertanto:
![]()
e cioè:

Scaricate i due software sulle permutazioni presenti qui in alto e provate altri esempi.![]() Continua...
Continua...