Option Club
Gioco Equo
TEORIA

Gioco Equo
Speranza Matematica o Valore atteso
Il concetto più importante allorché si vogliono prendere delle decisioni razionali sulla convenienza o meno di partecipare sistematicamente a un dato gioco, e’ sicuramente quello della speranza matematica o valore atteso.
Motiviamo l’utilità’ di tale concetto attraverso il classico esempio della moneta.
Supponiamo di dover decidere di partecipare ad un gioco in cui viene lanciata in aria per due volte di seguito una moneta “perfetta” e le cui vincite offerte dal gestore del gioco sono le seguenti:
- due teste consecutive - si vincono 2 €
- due croci consecutivi - si vincono 3 €
- una testa e una croce - si perdono 4 €
E’ conveniente giocare? E, se decidessimo di scommettere, quanto ci aspetteremmo di vincere o perdere mediamente protraendo il gioco?
Per rispondere a questi due quesiti, dobbiamo anzitutto conoscere il numero dei casi possibili.
Sappiamo dall’esempio precedente che essi sono esattamente quattro:
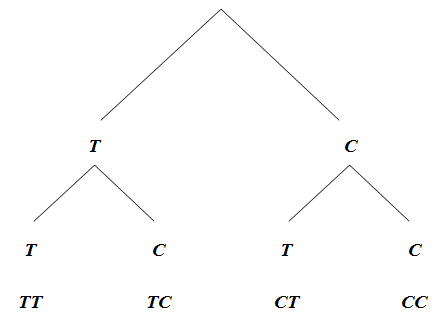
Per inciso, questo schema prende il nome di diagramma ad albero (così chiamato a causa della sua struttura ramificata) e serve per enumerare tutti i possibili esiti di una serie di esperimenti, ciascuno dei quali può avere solo un numero finito di esiti.
Quindi – mediamente – giocando quattro partite, noi otterremo: “due teste” una volta, “due croci ancora una vota e “una testa e una croce” due volte.
In queste quattro partite il nostro guadagno effettivo sarà:
![]()
perderemo cioè 3 € mediamente ogni quattro partite. Quindi in definitiva non ci conviene scommettere in un simile gioco; tuttavia se decidessimo di farlo dovremmo aspettarci di perdere, ogni partita, 1/4 di 3 €, ossia 75 centesimi.
Per ottenere questo valore (atteso) in maniera più diretta potevamo moltiplicare le probabilità relative di ciascun evento per il corrispondente premio facendo precedere quest'ultimo dal segno negativo in caso di perdita.
![]()
Possiamo a questo punto ricavare un metodo generale per calcolare la speranza matematica.
Supponendo che E1, E2, E3,. . .En siano eventi tra loro incompatibili (nel senso che due di essi non possono mai verificarsi contemporaneamente); P1, P2, P3,.. .Pn le relative probabilità e R1, R2, R3,. ..Rn i corrispondenti valori-premio, il "guadagno medio" o speranza matematica "S" e' data:
![]()
Ora, come sapete, in un gioco organizzato per avere diritto a partecipare si paga una somma S (“Posta”) prima di iniziare a giocare, quindi le vincite sono lorde.
Supponiamo che S sia il prezzo per partecipare a un determinato gioco e p la probabilità di vincere una certa somma Q; allora è come dire che con probabilità p guadagneremo esattamente Q - S (la vincita meno la puntata), mentre con probabilità 1 - p guadagneremo - S, cioè perderemo la posta.
Possiamo schematizzare la nostra giocata nel seguente modo:
Vincita |
Perdita |
|
|
|
|
Calcoliamo la speranza matematica:
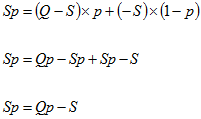
Esempio

Supponiamo di scommettere 1€ per un certo numero di colpi su un singolo numero ad una roulette francese che cosa dovremmo aspettarci in media?
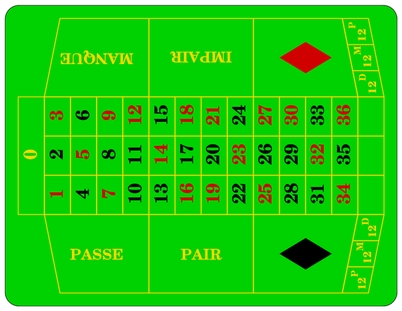
Ricordiamo prima brevemente le regole della roulette francese. Su una ruota sono disposti i numeri da 1 a 36, metà rossi e metà neri, con in più lo 0.
Gli stessi numeri sono riportati su un tappeto verde - allineati su tre colonne - dove sono indicate tra l'altro alcune delle scommesse possibili:
- Il Numero in pieno è pagato 35 volte la posta + la posta;
- Il Cavallo (2 numeri), 17 volte + la posta;
- La Terzina (3 numeri), 11 volte + la posta;
- Il Carré (4 numeri), 8 volte + la posta;
- La Sestina (6 numeri), 5 volte + la posta;
- La Dozzina (12 numeri), 2 volte + la posta;
- La Colonna (12 numeri), 2 volte + la posta;
- Chances semplici (Rosso - Nero - Pari - Dispari - Manque – Passe, 18 numeri) pagati alla pari, cioè 1 volta la posta + la posta.
Come si vede la vincita Q è data dal rapporto tra 36 e la quantità di numeri coperti dalla puntata.
Per esempio, per un numero in pieno Q = 36, per la dozzina Q = 3, per le puntate sulle chances semplici Q = 2.
Se esce lo zero, le puntate effettuate sulle chances semplici vengono congelate e restituite se al turno successivo esce quanto puntato; oppure possono essere direttamente divise con il banco. Tutte le altre scommesse sono irrimediabilmente perse tranne – ovviamente – quelle effettuate sullo zero.
Se l'esito è favorevole, ossia se esce il numero puntato, si vincono 36€ (35 volte la posta + la posta puntata), se invece non esce, si perde 1€ (la posta). Inutile dire che la vincita netta è 36-1=35€.
Che cosa succede mediamente? Applicando la formula vista in precedenza abbiamo:
![]()
Ciò significa che il giocatore, facendo questo tipo di scommessa, perderà in media più di 2,7 centesimi di euro.
Ovviamente il giocatore non perderà mai effettivamente 2,7 centesimi di euro. Ad ogni puntata vincerà o perderà 1€. Ma, continuando a ripetere un gran numero di volte questa scommessa, sul lungo periodo egli perderà in media circa 2,7% dell'intero capitale investito.
Si può dimostrare che alla roulette ogni scommessa, oppure ogni combinazione di scommesse, ha sempre la stessa speranza matematica negativa, cioè si ha la certezza, da un punto di vista probabilistico, di perdere mediamente 2,7 centesimi per ogni euro scommesso, tranne - naturalmente - le puntate sulle chances semplici il cui meccanismo di recupero fa si che la perdita sia leggermente minore, solo 1,35 centesimi per ogni euro giocato.![]() Continua ...
Continua ...