Option Club

Prima di prendere delle decisioni relative all’opportunità’ o meno di partecipare sistematicamente a un dato gioco e’ importante chiedersi se ne valga veramente la pena, se cioè le vincite potranno essere quanto meno uguali alle perdite.
In sostanza dobbiamo chiederci se si tratta o no di un gioco equo.

Un gioco si dice equo quando il guadagno medio prevedibile (quello che in termini matematici prende il nome di speranza matematica o valore atteso) e’ nullo per ciascun giocatore.

In altre parole, nessun giocatore risulta avvantaggiato nel lungo periodo rispetto all’altro.

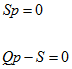
ovvero se

Un generico gioco risulua equo se la posta che siamo disposti a pagare per parteciparvi è uguale al prodotto della vincita Q per la probabilità p di ottenerla.

La formula precedente può anche essere sritta in questo modo:

Allora una scommessa risulta equa se la vincita Q che possiamo realizzare è uguale a 1/p volte la posta che abbiamo pagato per parteciparvi. Se giochiamo 1€ (cioè S=1) allora la vincita equa è 1/p.

Immaginiamo che due giocatori, basandosi sul lancio di un dado, disputino una serie di partite scommettendo il primo, sulla sortita di un numero dispari, l’alto, su quella di un numero pari.

Ora, considerando che il lancio di un solo dado comporta 6 risultati mutuamente esclusivi (nel senso che la comparsa di una faccia esclude la possibilità che possano verificarsi le altre) e ugualmente verosimili (dado non truccato), e che sia l’evento A (il verificarsi di un numero dispari 1, 3, 5) sia quello B (il verificarsi di un numero pari 2, 4, 6), sono costituiti ciascuno da 3 casi favorevoli, ne deriva che esiste la stessa probabilità ( 3/6 = 0,5 ) che si verifichi uno dei due eventi.
Supponendo ancora che la posta sia la stessa per chi vince e per chi perde (per esempio 1€), e’ chiaro che nessuno dei due scommettitori può aspettarsi a priori, da questo tipo di gioco, un vantaggio sistematico.

Infatti, dalla formula della speranza matematica, abbiamo:

Come chiunque avrebbe potuto anticipare senza troppi calcoli, giocando a “pari e dispari” con un dado, il guadagno medio prevedibile risulta nullo.

Indice di Equità

Dalla formula del gioco equo

possiamo ricavare il cosiddetto “Indice di Equità”:

Dove:

• p rappresenta la probabilità di vincita;
• Q e’ la vincita lorda, ossia comprensiva della posta (nel Totocalcio e’ la quota di vincita).
• S e’ la posta (la somma scommessa).

Questo indice permette stabilire a priori se un determinato gioco sia equo, vantaggioso o iniquo a seconda che esso sia rispettivamente uguale, maggiore o minore di uno.

Chiariamo meglio questo concetto riprendendo l’esempio precedente.

Giocando a “pari e dispari” con il lancio di un dado, abbiamo che le probabilità di vincere sono pari a 0,5; esattamente uguali sono le probabilità di perdere.

Per stabilire se questo gioco sia equo, vantaggioso o iniquo, e’ sufficiente moltiplicare 0,5 per la vincita diviso la posta.

Per esempio, se scommettessimo 1€ (posta) e la vincita fosse di 2€, il gioco risulterebbe equo. Infatti:

Qualora scommettessimo 1€ e la vincita fosse invece di 3€, il gioco risulterebbe vantaggioso:

Infine, se scommettessimo 1€ e la vincita fosse di 1€, il gioco risulterebbe iniquo (svantaggioso):

Durante lo svolgimento di un gioco equo, si potranno presentare oscillazioni di guadagno netto in più o in meno che rendono il gioco in qualche modo praticabile (infatti, se tutto fosse prevedibile non avrebbe senso giocare); tali scarti possiedono due caratteristiche (per lo meno quando le probabilità di vincita e di perdita sono esattamente uguali):

• la prima e’ che l’entità’ degli scarti positivi e quella degli scarti negativi hanno la stessa probabilità di verificarsi.

• la seconda e’ che l’ampiezza massima che puo’ raggiungere una oscillazione per un determinato numero di giocate, quasi sicuramente non può superare un certo limite; ciò ci consente, pur avendo scarse disponibilità finanziarie, di protrarre il gioco per tutto il ciclo delle giocate programmato (vedremo poi in che modo).

E’ importante sottolineare che, per avere un gioco equo non e’ indispensabile che ciascun giocatore possieda la stessa probabilità’ di vincere o di perdere.

Si consideri per esempio una serie di partite nelle quali un giocatore deve scommettere su due lanci consecutivi di una moneta non truccata e che vinca quando compaiono due “teste”.

In questo caso la probabilità di vincita e’ 0,25 (due “teste” consecutive), mentre quella di perdita (evento complementare) e’ 0,75. Ebbene, se il giocatore quando vince riceve un premio pari al triplo della sua posta e, quando perde, perde soltanto la posta, allora il gioco e’ ancora equo; anche in questo caso, infatti, il guadagno medio prevedibile risulta nullo.
Se ad esempio la posta e’ 1€ e la vincita e’ di 3€, la somma che mediamente si può sperare di vincere e’ 0,25 x 3=0,75 mentre quella che mediamente si rischia di perdere e’ 0,75 x (-1)=-0,75, quindi esattamente la stessa ma di segno contrario.

Inutile dire che anche qui si verificheranno degli scarti positivi e negativi che, nel caso specifico, avranno una diversa probabilità di verificarsi.

La tabella sottostante mostra i risultati relativi alle giocate semplici effettuate al gioco del Lotto

Se giocando alla roulette perdevano mediamente 2,7% per ogni euro scommesso, al gioco del Lotto, nel caso più favorevole, perdiamo il 37,58% per ogni euro scommesso. Ciò fa ritenere la roulette molto più onesta rispetto al gioco del Lotto.

Indietro