CC1 - Option Club
Menu principale:
- HOME
- CHI SIAMO
- FORUM
- TEORIA
- DISCLAIMER
- PARTNERS
- DOWNLOAD
CC1
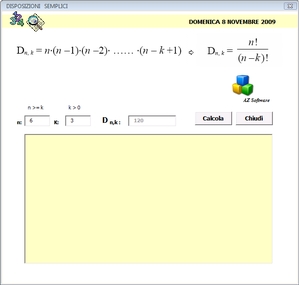
Le disposizioni semplici di n elementi in gruppi di k (quando k è minore di n) sono tutti i possibili raggruppamenti che si possono formare con gli n elementi, prendendone ogni volta una quantità pari a k; ogni gruppo differisce dagli altri o per l’ordine o per gli elementi.
Riprendiamo l’esempio precedente; supponiamo ora che i posti disponibili non siano più 4 ma soltanto 2. In questo caso dunque soltanto 2 persone potranno sedersi al tavolo; ripetendo il ragionamento fatto in precedenza avremo 4 diversi possibili modi di occupare il primo posto e 3 diversi possibili modi di occupare il secondo posto che rappresenta ora l’ultimo posto disponibile. Avremo dunque che i diversi possibili modi per disporre le 4 persone a gruppi di 2 intorno al tavolo sono dati da 4 x 3 = 12. Tale infatti è il numero delle disposizioni di 4 elementi presi a gruppi di due.
In generale possiamo dire che il numero delle disposizioni semplici di n elementi presi in gruppi di k è dato dal prodotto dei primi k numeri decrescenti a partire da n, esso compreso. In formula scriveremo:
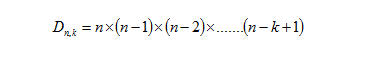
Da cui:
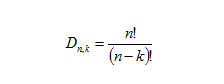
Così, ad esempio, se vogliamo calcolare 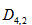 nei due modi descritti, si ha:
nei due modi descritti, si ha:
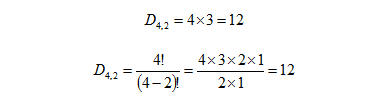
Immaginando che le 4 persone siano contrassegnate dalle lettere minuscole a, b, c, d le 12 disposizioni sono:
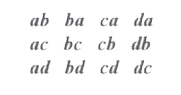

In quanti modi diversi si possono piazzare i primi 3 cavalli di una corsa con 20 partenti?
Vi sono 20 scelte per chi vince la corsa, 19 per il primo piazzato (cavallo che arriva secondo) e 18 per il secondo piazzato (cavallo che arriva terzo).
Pertanto vi sono 20 x 19 x 18= 6840 diversi ordini di arrivo validi, per esempio, per vincere matematicamente una corsa Tris con 20 cavalli in partenza.
Applicando la formula delle disposizioni semplici avremmo ottenuto lo stesso risultato:
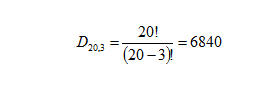
A conclusione possiamo dire pertanto che le permutazioni e le disposizioni semplici di un certo numero di n elementi sono il numero di possibili gruppi diversi che si possono formare prendendo ogni volta rispettivamente tutti gli elementi disponibili o solo una parte.