CC2 - Option Club

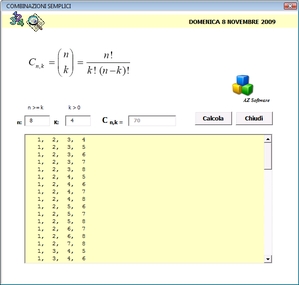
Da non confondersi con le disposizioni sono le combinazioni (semplici).

Infatti, le combinazioni di n elementi presi a gruppi di k sono i possibili raggruppamenti che si possono formare con gli n elementi dati, tali che ogni gruppo differisca dagli altri per almeno un elemento.

Nelle combinazioni - in altre parole - non ha più alcuna importanza l’ordine con cui si succedono gli elementi in ciascun gruppo.

Consideriamo ancora, come esempio, il caso che vi siano 4 persone da disporre in soli 2 posti. Se teniamo conto dell’ordine di disposizione abbiamo - come visto in precedenza - 12 disposizioni; ma se si vuole sapere semplicemente il numero dei possibili gruppi di persone differenti che possono trovare posto intorno al tavolo dovremo considerare le combinazioni, che - nell’esempio specifico - sono soltanto 6. Il numero delle combinazioni è dunque minore rispetto a quello delle disposizioni di un ugual numero di elementi in gruppi delle medesime dimensioni, in quanto l’ordine di successione degli elementi non rappresenta più un carattere discriminante.

Infatti due o più gruppi considerati distinti nelle disposizioni, perché caratterizzati da un ordine di successione diverso dei loro elementi, non saranno più tali nelle condizioni in cui non si tiene conto dell’ordine, e dovranno essere considerati come un solo gruppo distinto.

Ora, per ottenere il numero di combinazioni, se i gruppi sono formati da 2 persone ciascuno, le permutazioni di questi saranno proprio il numero di casi da non considerare (perché differenti solo per l’ordine).

Quindi il numero di combinazioni di 4 persone a 2 a 2 è uguale al numero delle disposizioni di 4 persone a 2 a 2 (12) diviso il numero di permutazioni di 2 persone (2! = 2). Generalizzando abbiamo:

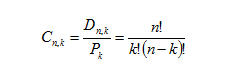
Immaginando sempre che le 4 persone siano contrassegnate dalle lettere minuscole a, b, c, d  le 6 combinazioni sono:

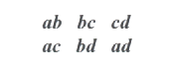
Calcolare il numero di ambi, terni, quaterne, cinquine possibili a Lotto.

Il Gioco del Lotto è un gioco molto popolare in Italia. In un urna ci sono 90 palline numerate da 1 a 90. Vengono estratte, una dopo l'altra e senza reimbussolamento, 5 palline.

Si vince se si riesce ad indovinare, in una giocata precedente l'estrazione, una coppia di numeri (ambo), una terna di numeri (terno), una quaterna di numeri (quaterna), i 5 numeri (cinquina).

Qui l’ordine non è importante; in tutti i casi si tratta di combinazioni semplici di 90 elementi presi rispettivamente 2, 3, 4 o 5 alla volta.

Quindi possiamo scrivere:



Come si vede, se da una parte è relativamente semplice realizzare un ambo, diventa sempre più difficile realizzare un terno, una quaterna, una cinquina al Lotto (quasi 44 milioni di cinquine possibili!).

Sarebbe interessante anche esaminare come lo Stato, gestore del gioco, ricompensa (si fa per dire...) le eventuali vincite.
Ma questo è un argomento che vedremo successivamente quando parleremo di gioco equo.

Scaricate il software sulle combinazioni semplici raffigurato qui a lato e provate altri esempi.


 

Indietro

Avanti