CC3 - Option Club

Il numero delle combinazioni semplici, Cn,k  è spesso indicato con il simbolo seguente:

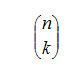
che si legge « n su k » e viene detto coefficiente binomiale perché se ne fa uso nello sviluppo della potenza di un binomio.

Quindi, per definizione possiamo scrivere:

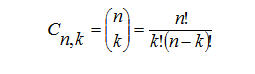
Ora, per fissare le idee, scriviamo in modo ordinato il valore di tutti i coefficienti binomiali.
In altre parole dato che il valore di k deve essere compreso fra 0 e n, fissato n e facendo variare k da k = 0 fino a k = n, abbiamo la seguente tabella dei valori di Ck,n per i primi 8 valori di n:

Il gruppo di numeri che ne deriva viene chiamato Triangolo di Tartaglia o anche Triangolo di Pascal.

Sicuramente avrete già notato qualche peculiarità di questo triangolo: intanto che ogni riga inizia e termina con 1; gli altri valori si ottengono sommando i due elementi della riga precedente immediatamente sopra e a sinistra rispetto all’elemento considerato.

Ad esempio l’elemento 28, nella riga 8 è ottenuto come somma dei due numeri 7 e 21 che si trovano immediatamente al di sopra di esso, ossia:

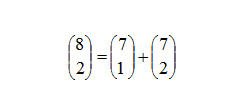
Generalizzando possiamo scrivere:

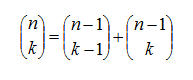
Ecco come si ottengono le prime 4 righe del Triangolo di Tartaglia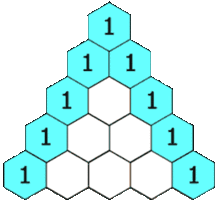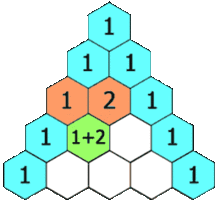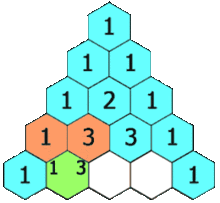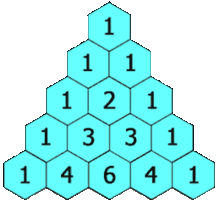

Ora, se osserviamo i numeri di ogni riga, scopriamo un’altra caratteristica del Triangolo di Tartaglia:
i numeri di ogni riga coincidono con i coefficienti numerici dello sviluppo di della generica potenza di un binomio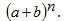

Per esempio, lo sviluppo:

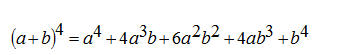
ha i coefficienti numerici 1, 4, 6, 4 e 1, corrispondenti ai valori forniti dalla 4ª riga del triangolo.
Ecco il  motivo perchè tali numeri si chiamano anche coefficienti binomiali.

Potete scaricate il software sul Triangolo di tartaglia raffigurato qui a lato e provate altri esempi.


 

Indietro

Avanti