CC4 - Option Club

Permutazioni, disposizioni e combinazioni con ripetizione

Ci occuperemo adesso delle disposizioni, delle permutazioni e delle combinazioni con ripetizione.

Per spiegare questi aspetti più complessi del calcolo combinatorio, in cui sono presenti le ripetizioni di simboli o di elementi uguali, ci serviremo di tre esempi.

• Calcolare tutte le diverse sequenze di simboli testa e croce che si possono formare con tre lanci consecutivi di una moneta.
  

• Trovare tutti gli anagrammi della parola TOTO.
  

• In quanti modi si possono distribuire caramelle di 4 gusti differenti a 2 bambini considerando che uno stesso gusto può essere dato più di una volta?
  

Soluzione 1. Complessivamente possono essere formate 8 figure che derivano dal prodotto degli eventi elementari del primo lancio (Testa e Croce) per quelli del secondo e del terzo; cioè:

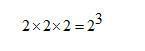
(2 rappresenta il numero delle facce della moneta e 3 quello dei lanci).

A sinistra l'elenco completo degli esiti possibili.

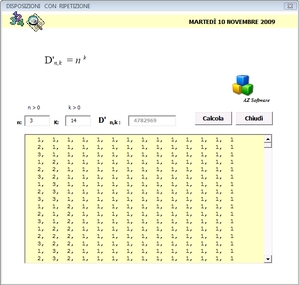
Generalizzando, se consideriamo n elementi, anche ripetuti, a gruppi di k, le disposizioni con ripetizione sono uguali a:

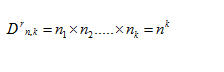
Scaricate il software sulle disposizioni con ripetizione raffigurato qui a lato e provate altri esempi.


 

Indietro

Avanti