CC5 - Option Club
Menu principale:
- HOME
- CHI SIAMO
- FORUM
- TEORIA
- DISCLAIMER
- PARTNERS
- DOWNLOAD
CC5

Con le disposizioni con ripetizione possiamo calcolare, per esempio, il numero delle colonne che è necessario giocare, nel gioco del Totocalcio, per fare con certezza il “Quattordici”.
Se spostiamo l’argomento dalla moneta al Totocalcio, il discorso diventa apparentemente più difficile.
Innanzitutto è importante raccogliere tutte le informazioni disponibili. Sappiamo che per partecipare ad un qualsiasi Concorso Totocalcio bisogna esprimere un pronostico -
Per poter rappresentare questa previsione abbiamo a disposizione tre simboli:
il segno “1”: che indica la vittoria della squadra che gioca in casa;
il segno “X”: attraverso il quale è possibile esprimere il risultato di parità delle due squadre contendenti;
il segno “2”: che indica la vittoria della squadra che gioca in trasferta.
Poiché -
Ne deriva che tutte le configurazioni possibili, su un campo di 14 varianti triple, saranno il prodotto di 3 moltiplicato per se stesso 14 volte consecutive, ovvero una potenza in base 3 ed esponente 14 che da come risultato:
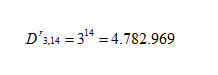
Possiamo così affermare con assoluta certezza che per fare “Quattordici” al Totocalcio sono necessarie esattamente 4.782.969 colonne.
Da quanto detto si ricavava una formula matematica di validità generale, attraverso la quale è possibile sapere, senza bisogno di preventivi sviluppi, di quante colonne si compone un qualsiasi sistema integrale formato da un certo numero di fisse, doppie e triple.
Supposto che “nvd” sia il numero di varianti doppie e “nvt” il numero di varianti triple, il numero di colonne che compongono un generico sistema integrale è dato:
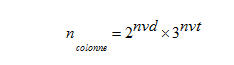
Utilizzando questa equazione matematica, ci è sembrato opportuno determinare per ciascuna combinazione di doppie e triple il numero di colonne sviluppate integralmente e riportarle nella seguente tabella:
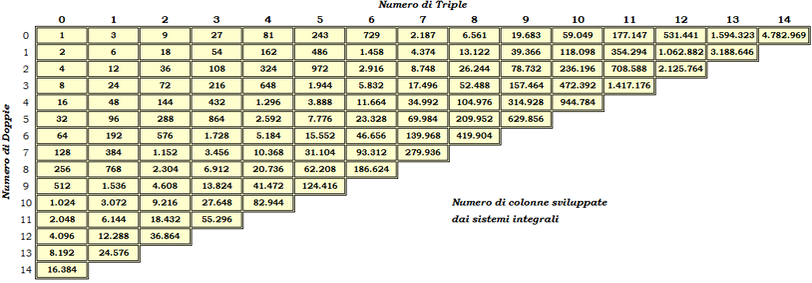
Per esempio un sistema integrale di 3 doppie e 4 triple è composto da 648 colonne.

