CC6 - Option Club
Menu principale:
- HOME
- CHI SIAMO
- FORUM
- TEORIA
- DISCLAIMER
- PARTNERS
- DOWNLOAD
CC6
Soluzione 2. Gli anagrammi che si possono formare con la parola TOTO sono 6 e precisamente:

Se le lettere fossero state diverse l’una dall’altra, avremmo avuto:
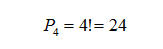
cioè 24 permutazioni; nel nostro caso vi sono però due coppie di lettere uguali, TT e OO, ognuna delle quali può essere sistemata in 2! modi; pertanto si hanno 2! x 2! = 4 ripetizioni.
Possiamo allora scrivere:
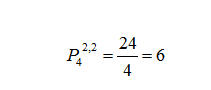
Siamo così pervenuti alla formula matematica che ci permette di calcolare il numero di permutazioni con ripetizione di un qualsiasi gruppo di elementi misti:
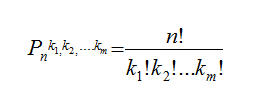
la quale ci dice semplicemente che: le permutazioni con ripetizione di un gruppo di n elementi di cui K1 uguali, k2 uguali, ...km uguali (con K1 + k2 +...km = n) sono uguali al fattoriale di n diviso il prodotto dei fattoriali degli elementi uguali fra loro.
Per inciso, questa formula serve per calcolare, come adesso vedremo, il numero di colonne delle formule derivate.
Considerato un sistema di “n” partite, la formula derivata rappresenta l’insieme di colonne che contengono una quantità costante di segni “1”, “X” e “2” e cioè n1 segni “1”, nx segni “X”, n2 segni “2”. Si usa rappresentare la formula derivata nel seguente modo n1 – nx – n2 , dove n1 – nx – n2 (separati convenzionalmente da un trattino) sono tre numeri interi che rappresentano rispettivamente la quantità dei segni “1”, “X” e “2”.
Inutile dire che: n1 + nx + n2 = n
Volendo fare un esempio costituito da tutte e quattordici le partite inserite in schedina (n = 14), la terna 7 -
La formula derivata costituisce uno dei due elementi di differenziazione delle colonne del Totocalcio; l’altro elemento è la disposizione dei simboli nell’ambito delle quattordici caselle. Pertanto, colonne diverse possono presentare la stessa formula derivata, differendo tra loro unicamente per una diversa disposizione dei simboli. Nasce quindi la necessità di conoscere, per ciascuna combinazione di segni, il numero di colonne possibili. Tale valutazione viene effettuata attraverso la formula delle permutazioni con ripetizione.
Per i nostri scopi la formula può essere adattata nel seguente modo:
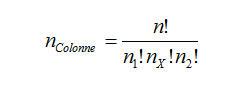
Dove:
“n” indica il numero delle partite considerate (nel nostro caso 14).
n1 –nx – n2 , sono tre numeri che rappresentano nell’ ordine la quantità dei segni “1”, “X” e “2”;
Per conoscere ad esempio il numero di colonne appartenenti alla citata formula derivata 7 -
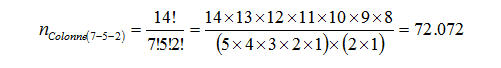
Ci è sembrato opportuno -
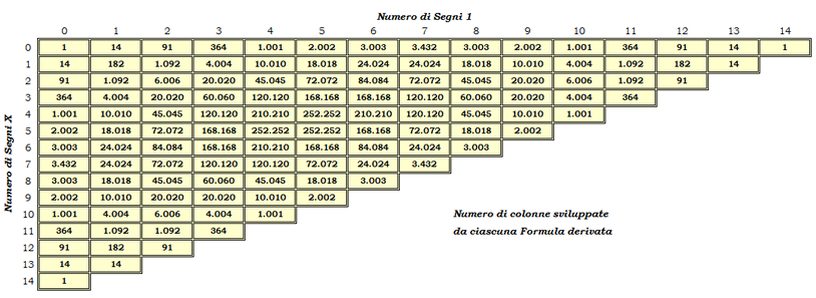

Soluzione 3. Immaginiamo che le caramelle appartenenti ai 4 gusti siano contrassegnate dalle lettere a, b, c, e d; i modi possibili con cui queste caramelle possono essere distribuite ai 2 bambini (supponendo di poter dare uno stesso gusto più di una volta) sono 10 e precisamente:
...............................aa ....ab ....ac ....ad
...............................bb ....bc ....bd
...............................cc ....cd
...............................dd
Le combinazioni con ripetizione di n elementi presi a gruppi di k sono i possibili raggruppamenti che si possono formare con gli n elementi dati (ogni elemento può comparire più di una volta in un gruppo), tali che ogni gruppo differisca dagli altri per almeno un elemento.
La formula che dà il numero delle combinazioni con ripetizione di n elemento di classe k è:
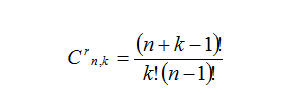
Nell’esempio precedente si ha: