CC7 - Option Club
Menu principale:
- HOME
- CHI SIAMO
- FORUM
- TEORIA
- DISCLAIMER
- PARTNERS
- DOWNLOAD
CC7
Enunciati i due teoremi fondamentali del calcolo delle probabilità e chiariti i concetti essenziali del calcolo combinatorio, possiamo risolvere qualche problema più complesso di calcolo delle probabilità.
Un’ urna contiene 5 biglie numerate dall’ 1 al 5. Qual è la probabilità che in due estrazioni successive si presenti prima una biglia contrassegnata da un numero pari e poi una con un numero dispari se dopo la prima estrazione si rimette la pallina nell’urna?
In questo caso bisognerà ovviamente applicare il teorema delle probabilità composte per eventi indipendenti in quanto la biglia viene rimessa nell’urna dopo la prima estrazione; la probabilità pertanto sarà:
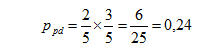

Qual è invece la probabilità che le due biglie estratte siano una pari ed una dispari? In questo caso bisognerà applicare il teorema delle probabilità composte per eventi indipendenti e il teorema delle probabilità totali per eventi incompatibili; cioè:
per eventi indipendenti in quanto la biglia viene rimessa nell’urna dopo la prima estrazione; la probabilità pertanto sarà:
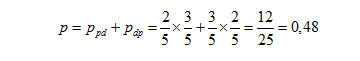
Nell’ipotesi che la prima biglia estratta non venga rimessa nell’urna, la probabilità che si presenti prima una biglia pari e poi una dispari sarà invece:
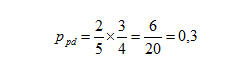
mentre la probabilità che le due biglie estratte siano una pari ed una dispari sempre nell’ipotesi che la prima biglia estratta non venga rimessa nell’urna, sarà:
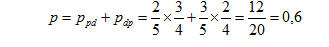

Siamo ora in grado di dare anche una risposta al problema del Cavaliere de Méré.
Come si ricorderà, il quesito riguardava sostanzialmente il confronto tra le probabilità di due eventi. Il primo di essi si verifica quando, in quattro lanci di un dado, appare almeno una volta la faccia contrassegnata con il 6, mentre il secondo si verifica quando, su ventiquattro lanci di due dadi, si presenta almeno una volta una coppia di 6. Ebbene, con semplici calcoli si dimostra che, mentre la scommessa alla pari effettuata sul primo evento è matematicamente vantaggiosa, la stessa scommessa realizzata sul secondo evento è assolutamente svantaggiosa.
Infatti, se p 1/6 è la probabilità di fare 6 lanciando un dado, quella di non fare nessun 6 in quattro lanci consecutivi, considerando che gli eventi sono indipendenti, è:
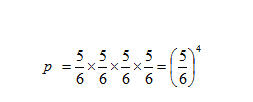
Ora, poiché siamo interessati all’evento complementare, cioè quello di ottenere almeno un 6 in quattro lanci di un dado, la probabilità cercata risulta essere uguale:
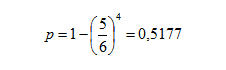
Come si vede essa è maggiore di 1/2 per cui una scommessa alla pari su tale evento risulta alla lunga vincente.
Utilizzando lo stesso ragionamento nel secondo caso, calcoliamo prima la probabilità di non fare un doppio 6 lanciando ventiquattro volte due dadi:
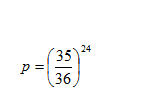
e poi quella di ottenere l’evento complementare:
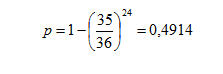
Questo secondo tipo di scommessa giocata alla pari risulta decisamente sfavorevole per il fatto di avere una probabilità minore di 1/2.
Proviamo ad impostare lo studio della probabilità di vincita del cavaliere de Méré e a verificare i risultati con un programma che utilizza un generatore di numeri casuali. Il programma simula n partite del gioco proposto dal Cavaliere de Méré, conta quante partite sono state vinte, e calcola poi la frequenza relativa del numero di vittorie (ossia la probabilità di vincere calcolata secondo la concezione frequentista). Eseguendo il programma per valori di n elevati si noterà che i risultati si avvicinano alle probabilità teoriche calcolate in maniera analitica.
Ecco i risultati ottenuti con una simulazione di un milione di lanci.
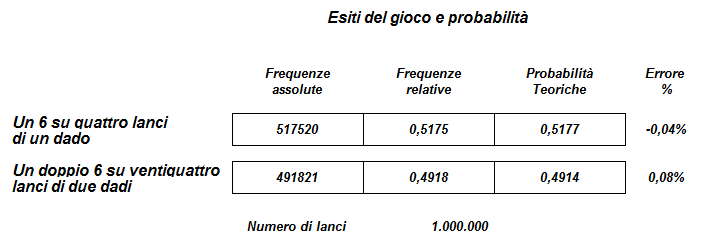
Cliccando sull’icona del logo a sinistra potete scaricare il software relativo e provare altre simulazioni.
