Probabilità 1 - Option Club
Menu principale:
- HOME
- CHI SIAMO
- FORUM
- TEORIA
- DISCLAIMER
- PARTNERS
- DOWNLOAD
Probabilità 1
In ogni esperimento casuale, dato che gli esiti non sono perfettamente determinabili a priori, non potremo mai sapere se un determinato evento si presenterà oppure no. Per esprimere il grado di attendibilità circa il suo verificarsi o probabilità è utile assegnare un numero compreso tra 0 e 1. Se siamo sicuri che l’evento si presenterà, diremo che la sua probabilità è pari al 100% o ad 1 (evento certo). Se invece siamo sicuri che l’evento non si verificherà, diremo che la sua probabilità è 0 (evento impossibile).
Se, ad esempio, in un determinato esperimento casuale la probabilità di un evento è ¼, diremo che esso ha una chance de 25% di verificarsi e una chance del 75% contraria.
Diciamo subito che non esiste una definizione di probabilità completamente soddisfacente. La probabilità – infatti – è uno di quei concetti elusivi che virtualmente ognuno conosce e che applica più o meno inconsciamente in quasi tutte le azioni quotidiane, ma che è pressoché impossibile definire in maniera accettabile.
Tuttavia, pur essendo un concetto intuitivo, dobbiamo dare comunque una definizione di probabilità.
A tale riguardo ci sono due importanti correnti di pensiero predominanti: la prima oggettivista (definizione classica, definizione frequentista) che assegna al concetto di probabilità un contenuto oggettivo e la seconda soggettivista che gli attribuisce invece un significato soggettivo. Per i nostri scopi la concezione oggettivista è più che sufficiente.
La probabilità che si verifichi un evento è uguale al rapporto tra il numero casi favorevoli e il numero dei casi possibili, purché questi siano tutti ugualmente verosimili. Questa definizione contiene in sé un apparente vizio; infatti, riflettendoci sopra un attimo, ci accorgiamo che non sempre si può stabilire priori quali siano i casi ugualmente verosimili se non attraverso la stessa definizione probabilità. Per superare questo ostacolo si usa specificare nei classici esempi del calcolo delle probabilità basati su lancio di monete, lancio di dadi e gioco delle carte, la dizione non truccato e ben mescolato rispettivamente per le monete ed dadi e per il mazzo di carte; ciò permette di soddisfare la richiesta di casi “ugualmente verosimili “.
Supponiamo di voler determinare la probabilità che lanciando una moneta per aria si presenti la faccia testa.
Ci sono due modi ugualmente possibili in cui la moneta può ricadere (testa e croce) e di questi due, testa può presentarsi in un solo modo.
Pertanto la probabilità d’uscita della faccia in questione è:
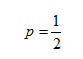
al numeratore compare l’evento favorevole (testa) e al denominatore tutti quelli possibili (testa e croce). La probabilità di ottenere croce (evento complementare) si ottiene sottraendo la probabilità d’uscita della faccia testa all’unità; dunque è la medesima.
Per estensione se indichiamo con p la probabilità che un evento si verifichi, 1 -
Possiamo quindi affermare che ciascuna faccia di una moneta, ad ogni lancio, ha il 50% di probabilità d’uscita.
Supponiamo adesso di lanciare in aria due volte di seguito una moneta “perfetta”, precisando con ciò che ognuna delle due facce possiede uguale probabilità di sortita, puntando sulla comparsa di due teste consecutive, che probabilità avremo di conseguire la vincita? Poiché i due lanci della moneta sono eventi indipendenti, nel senso che il risultato dell‘uno non ha niente a che vedere con il risultato dell’altro, la probabilità di avere la comparsa di due teste consecutive è data, come vedremo successivamente, dal prodotto delle singole probabilità elementari:

tuttavia, quello che volevo sottolineare in questo caso, è che lo stesso risultato poteva ottenersi valutando a priori il numero dei casi favorevoli e possibili che si verificano in due lanci consecutivi di una moneta; infatti, non potrà verificarsi altro che una delle seguenti combinazioni:
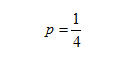
Lanci |
Primo |
Secondo |
Casi |
||
1° |
Testa |
Testa |
2° |
Testa |
Croce |
3° |
Croce |
Testa |
4° |
Croce |
Croce |
Come si vede l’unico caso favorevole è il primo. I casi possibili sono invece quattro cioè tanti quante sono le disposizioni con ripetizione di due elementi presi a due a due.
Pertanto, la probabilità di vincere puntando sulla comparsa di due teste consecutive in un doppio lancio di una moneta è:

